El Taller de Talento Matemático de Aragón (TTM) inicia su 7ª temporada. Se trata de una actividad extraescolar de asistencia libro y gratuita dirigida a estudiantes desde 3ºESO hasta 2ºBachillerato. Las sesiones se celebran cada dos ó tres semanas, los viernes, de 18h a 19:30h.
La primera sesión del curso 2010 - 2011 será el próximo viernes 22 de octubre de 18:00 a 19:30 horas.
3º y 4º ESO (Aula Magna de la Facultad de Ciencias): Magia y Matemáticas, por el mago Alejandro Hernández Nebra, "El Gran Alexander". (CPR Juan de Lanuza de Zaragoza y Asociación Mágica Aragonesa).
Bachillerato (Aula 5 del Edificio de Matemáticas): Preparación de la XLVII Olimpiada Matemática Española (I), por Eva Elduque Laburta y Adrián Rodrigo Escudero (Facultad de Ciencias de la Universidad de Zaragoza).
Toda la información e inscripciones en http://www.unizar.es/ttm/
Para contactar por correo electrónico ttm@unizar.es
viernes, 8 de octubre de 2010
martes, 4 de mayo de 2010
LAS 10 EMPRESAS ALIMENTARIAS CON MAYOR GASTO EN PUBLICIDAD
Se ha extraído, de la lista de las 1000 empresas que más invirtieron en anuncios en 2008, las 10 empresas alimentarias que más lo hacen:
- DANONE (8) 68 millones de euros.
- COCA COLA (15) 47,5 millones de euros.
- NESTLÉ (32) 31,0 millones de euros.
- HEINEKEN (37) 27 millones de euros.
- LECHE PASCUAL (44) 21,5 millones de euros.
- KELLOGG (56) 18,5 millones de euros.
- FERRERO IBERICA (61) 18 millones de euros.
- MAHOU (67) 17 millones de euros.
- SCHWEPPES (74) 16,0 millones de euros.
- KRAFT FOODS (77) 15,5 millones euros.
a) Representa la situación mediante el gráfico más conveniente
b) Calcula la media, la mediana y la desviación típica
c) Halla el tanto por ciento de empresas que se encuentran en los intervalos (x - s, x + s) y
(x - 2s, x + 2s). ¿Son similares a los correspondientes a una distribución normal?
viernes, 16 de abril de 2010
ESTADÍSTICA CON EXCEL
Tenéis que realizar individualmente la siguiente actividad con Excel
1. Escribe el enunciado del siguiente ejercicio
En una población de 25 familias se ha observado la variable X = "número de coches que tiene la familia" y se han obtenido los siguientes resultados:
0 1 2 3 1 0 1 1 1 4 3 2 2 1 1 2 2 1 1 1 2 1 3 2 1
2. Construye la tabla de frecuencias a partir de los datos
3. Representa mediante un diagrama de barras y un diagrama de sectores los datos
4. Calcula la media y la desviación típica
5. Halla la mediana y los cuartiles
Una vez que lo tengas todo guarda el archivo y mándamelo por correo antes del próximo 3 de mayo.
La corrección del ejercicio se realizará en clase el día 4 de mayo utilizando la Pizarra Digital.
1. Escribe el enunciado del siguiente ejercicio
En una población de 25 familias se ha observado la variable X = "número de coches que tiene la familia" y se han obtenido los siguientes resultados:
0 1 2 3 1 0 1 1 1 4 3 2 2 1 1 2 2 1 1 1 2 1 3 2 1
2. Construye la tabla de frecuencias a partir de los datos
3. Representa mediante un diagrama de barras y un diagrama de sectores los datos
4. Calcula la media y la desviación típica
5. Halla la mediana y los cuartiles
Una vez que lo tengas todo guarda el archivo y mándamelo por correo antes del próximo 3 de mayo.
La corrección del ejercicio se realizará en clase el día 4 de mayo utilizando la Pizarra Digital.
CIRCUNFERENCIAS CON WIRIS
Individualmente deberéis realizar la siguiente actividad:
1. Escribe la ecuación general de la circunferencia de centro (2, -3) y radio 4. Utiliza el programa Wiris para dibujar la gráfica de la ecuación obtenida y comprobar que es correcta. Guarda el archivo y envíamelo por correo.
2. ¿Cuál es el centro y el radio de la circunferencia de ecuación
x^2 + y^2 -6x + 8y -39 =0?
Igual que en el apartado anterior, utiliza Wiris para comprobar tu solución y mándame el archivo por correo.
Nota: para acceder al programa Wiris puedes clickar aqui.

1. Escribe la ecuación general de la circunferencia de centro (2, -3) y radio 4. Utiliza el programa Wiris para dibujar la gráfica de la ecuación obtenida y comprobar que es correcta. Guarda el archivo y envíamelo por correo.
2. ¿Cuál es el centro y el radio de la circunferencia de ecuación
x^2 + y^2 -6x + 8y -39 =0?
Igual que en el apartado anterior, utiliza Wiris para comprobar tu solución y mándame el archivo por correo.
Nota: para acceder al programa Wiris puedes clickar aqui.

Los ejercicios se tienen que presentar antes del puente de San Jorge para que se tengan en cuenta para la nota de evaluación.
La corrección se realizará el próximo día 26 de abril en el aula de Informática.
martes, 13 de abril de 2010
TRIGONOMETRÍA CON GEOGEBRA
La siguiente actividad es para realizarla individualmente. Esta actividad es puntuable y se tendrá en cuenta para la nota final de evaluación. Los archivos que vayas obteniendo has de mandarlos por correo electrónico a la dirección de gmail.
Abre el archivo "Angulos_Suplementarios.ggb" que guardamos el otro día en el aula Ramón y Cajal.
Desplaza el ángulo a para que el ángulo se vaya modificando y comprueba que se cumplen las relaciones entre las razones trigonométricas de dicho ángulo y su suplementario en el primer cuadrante tal y como vimos en clase para los ángulos 135º, 93º y 110º.
Haz una captura de pantalla para cada uno y después guárdala en Paint como "suplementarios_tunombre".
martes, 6 de abril de 2010
TRIGONOMETRÍA CON DESCARTES
Para repasar la Trigonometría vista en clase, vamos a utilizar el proyecto Descartes.
Podéis realizar la actividad en grupos de dos personas o, si alguien lo prefiere, individualmente.
Podéis realizar la actividad en grupos de dos personas o, si alguien lo prefiere, individualmente.
Clickando aquí, accederéis a una unidad didáctica interactiva del proyecto descartes incluida dentro del proyecto EDAD.
En la parte superior hay varias pestañas. Una vez que hayáis repasado los contenidos, iréis a la pestaña correspondiente a "Para enviar al tutor".
En la parte superior hay varias pestañas. Una vez que hayáis repasado los contenidos, iréis a la pestaña correspondiente a "Para enviar al tutor".
Deberéis contestar a todas las preguntas y, cuando lo hayáis terminado, deberéis enviármelo a la dirección de correo que os di a principio de curso. No olvidéis poner los nombres, por favor.
Os daré la puntuación obtenida en clase una vez lo hayamos resuelto.
Para aquellas personas que no puedan enviar las respuestas por correo electrónico por los motivos que sean, os pongo aquí las preguntas para que me las entreguéis por escrito en el Departamento.
1. Pasa a radianes o a grados, en cada caso, los siguientes ángulos:
a) 45º b) 2π/3 rad c) 240º d) 7π/4 rad
2. Calcula el seno y el coseno de un ángulo agudo sabiendo que su tangente vale 2.
3. Representa en la circunferencia goniométrica el ángulo α = −135º
4. La sombra de un árbol cuando los rayos del sol forman un ángulo de 50º con la
horizontal mide 8 m, ¿cuál es la altura del árbol?.
PRESENTACIÓN
En este blog vamos a trabajar los contenidos relativos al último trimestre para 4ºESO, preferiblemente de la opción B, aunque la parte de Estadística es válida para las dos opciones.
Vamos a presentar, de forma muy resumida algunos de los conceptos que ya se habrán visto y explicado en clase, para después plantear una serie de actividades que deberán ser realizadas por los alumnos y alumnas.
Los alumnos deberán realizar los ejercicios correspondientes, individualmente o en grupos de dos personas.
La formación de los grupos y el resultado de los ejercicios se enviarán por correo electrónico a la dirección que se dio a principio de curso. Aquellos alumnos o alumnas que no dispongan de correo electrónico, presentarán los ejercicios en papel.
jueves, 25 de marzo de 2010
PITÁGORAS
Pitágoras de Samos es, probablemente, el matemático más conocido a lo largo de la historia gracias al teorema que lleva su nombre: "En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos".
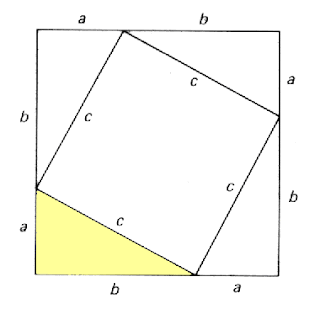
La siguiente imagen muestra una de sus demostraciones:
El área del cuadrado grande es (a+b)2 que, a su vez, es la suma de las áreas de un cuadrado de lado c y dos rectángulos de lados a y b, es decir, c2 + 2ab.
Pero el trabajo de Pitágoras y, más concretamente, de la escuela pitágorica, va más allá de este famoso teorema: ternas pitágoricas, números amigos, números figurados, ...
Si quieres conocer algo más a Pitágoras y su obra, puedes clicar aquí.
Actividades:
1. Averigua cuáles de los siguientes triángulos son rectángulos:
a) a = 17 cm , b = 10 cm , c = 22 cm
b) a = 35 m, b = 12 m , c = 37 m
c) a = 60 dm, b = 11 dm, c = 61 dm
La siguiente imagen muestra una de sus demostraciones:
El área del cuadrado grande es (a+b)2 que, a su vez, es la suma de las áreas de un cuadrado de lado c y dos rectángulos de lados a y b, es decir, c2 + 2ab.
Por lo tanto, (a+b)2 = c2 + 2ab Û a2 + b2 + 2ab = c2 + 2abÛ c2 =a2 + b2
Pero el trabajo de Pitágoras y, más concretamente, de la escuela pitágorica, va más allá de este famoso teorema: ternas pitágoricas, números amigos, números figurados, ...
Si quieres conocer algo más a Pitágoras y su obra, puedes clicar aquí.
Actividades:
1. Averigua cuáles de los siguientes triángulos son rectángulos:
a) a = 17 cm , b = 10 cm , c = 22 cm
b) a = 35 m, b = 12 m , c = 37 m
c) a = 60 dm, b = 11 dm, c = 61 dm
martes, 16 de marzo de 2010
INTERVALOS EN LA RECTA REAL
Los intervalos en la recta real son conjuntos de números reales comprendidos entre dos números reales dados.
Pueden ser de diferentes tipos:
Pueden ser de diferentes tipos:
Para más información y practicar con los intervalos ves a la siguiente dirección:
Suscribirse a:
Comentarios (Atom)

.jpg)